Giải bài tập SGK toán lớp 10 Chương 1
Giaoan.link chia sẻ các bài giải toán trong sách giáo khoa lớp 10 chương 1 – các bài tập về mệnh đề, tập hợp, các phép toán trong tập hợp giúp các bạn học sinh có tài liệu tham khảo trong học tập.
I- Bài tập mệnh đề – Trang 9, 10 SGK đại số 10
Bài số 1
Trong các câu sau, câu nào là mệnh đề, câu nào là mệnh đề chứa biến?
- a) 3 + 2 = 7;
- b) 4 + x = 3;
- c) x + y > 1;
- d) 2 – √5 < 0.
Hướng dẫn giải:
- a) Mệnh đề sai;
- b) Mệnh đề chứa biến;
- c) Mệnh đề chứa biến;
- d) Mệnh đề đúng.
Bài số 2
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu mệnh đề phủ định của nó:
a) 1794 chia hết cho 3;
b) √2 là một số hữu tỉ:
c) π < 3,15;
d) |-125| ≤ 0
Hướng dẫn giải:
- a) Đúng. Mệnh đề phủ định: “1794 không chia hết cho 3”.
- b) Sai. “√2 không phải là một số hữu tỉ”.
- c) Đúng. “π không nhỏ hơn 3, 15”. Dùng kí hiệu là: π ≥ 3,15.
- d) Sai. “|-125|>0”.
Bài số 3
Cho các mệnh đề kéo theo:
Nếu a và b cùng chia hết cho c thì a+b chia hết cho c (a, b, c là những số nguyên).
Các số nguyên có tận cùng bằng 0 đều chia hết cho 5.
Tam giác cân có hai đường trung tuyến bằng nhau.
Hai tam giác bằng nhau có diện tích bằng nhau.
a) Hãy phát biểu mệnh đề đảo của mỗi mệnh đề trên.
b) Phát biểu mỗi mệnh đề trên, bằng cách sử dụng khái niệm “điều kiện đủ”.
c) Phát biểu mỗi mệnh đề trên, bằng cách sử dụng khái niệm “điều kiện cần”.
Hướng dẫn giải:
a) Nếu a + b chia hết cho c thì a và b chia hết cho c. Mệnh đề sai.
Số chia hết cho 5 thì tận cùng bằng 0. Mệnh đề sai.
Tam giác có hai trung tuyến bằng nhau thì tam giác là cân. Mệnh đề đúng.
Hai tam giác có diện tích bằng nhau thì bằng nhau. Mệnh đề sai.
b) a và b chia hết cho c là điều kiện đủ để a+b chia hết cho c.
Một số tận cùng bằng 0 là điều kiện đủ để số đó chia hết cho 5.
Điều kiện đủ để một tam giác là cân là có hai đường trung tuyến bằng nhau.
Hai tam giác bằng nhau là điều kiện đủ để chúng có diện tích bằng nhau.
c) a + b chia hết cho c là điều kiện cần để a và b chia hết cho c.
Chia hết cho 5 là điều kiện cần để một số có tận cùng bằng 0.
Điều kiện cần để tam giác là tam giác cân là nó có hai trung tuyến bằng nhau.
Có diện tích bằng nhau là điều kiện cần để hai tam giác bằng nhau.
Bài số 4
Phát biểu mỗi mệnh đề sau, bằng cách sử dụng khái niệm “điều kiện cần và đủ”:
a) Một số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và ngược lại.
b) Một hình bình hành có các đường chéo vuông góc là một hình thoi và ngược lại.
c) Phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương.
Hướng dẫn giải:
a) Điều kiện cần và đủ để một số chia hết cho 9 là tổng các chữ số của nó chia hết cho 9.
b) Điều kiện cần và đủ để tứ giác là hình thoi là tứ giác là hình bình hành có hai đường chéo vuông góc với nhau.
c) Điều kiện cần và đủ để phương trình bậc hai có hai nghiệm phân biệt là biệt thức của nó dương.
Bài số 5
Dùng kí hiệu ∀, ∃ để viết các mệnh đề sau:
a) Mọi số nhân với 1 đều bằng chính nó;
b) Có một số cộng với chính nó bằng 0;
c) Một số cộng vớ số đối của nó đều bằng 0.
Hướng dẫn giải:
a)∀x ∈ R: x.1 = x;
b) ∃ x ∈ R: x + x = 0;
c) ∀x∈ R: x + (-x)= 0;
Bài số 6
Phát biểu thành lời mỗi mệnh đề sau và xét tính đúng sai của nó:
a) ∀x ∈ R: x2 > 0;
b) ∃ n ∈ N: n2 = n;
c) ∀n ∈ N: n ≤ 2n;
d) ∃ x ∈ R: x < 1/x.
Hướng dẫn giải:
a) ∀x ∈ R: x2 > 0 = “Bình phương của một số thực là số dương”. Sai vì 0 ∈R mà 02 = 0
b) ∃ n ∈ N: n2 = n = “Có số tự nhiên n bằng bình phương của nó”. Đúng vì 1 ∈ N, 12 = 1
c) ∀n ∈ N: n ≤ 2n = “Một số tự nhiên thì không lớn hơn hai lần số ấy”. Đúng.
d) d) ∃ x ∈ R: x < 1/x = “Có số thực x nhỏ hơn nghịch đảo của nó”. Mệnh đề đúng, chẳng hạn 0,5 ∈ R và 0,5 < 1/0,5.
Bài số 7
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó:
a) ∀n ∈ N: n chia hết cho n;
b) ∃x ∈ Q: x2 = 2;
c) ∀x ∈ R: x < x +1 ;
d) ∃x ∈ R: 3x = x2 + 1;
Hướng dẫn giải:
a) Có một số tự nhiên n không chia hết cho chính nó. Mệnh đề này đúng vì n = 0 ∈ N, 0 không chia hết cho 0.
b) ∃x ∈ Q: x2 = 2 = “Bình phương của một số hữu tỉ là một số khác 2”. Mệnh đề đúng.
c) ∀x ∈ R: x < x +1 = ∃x ∈ R: x ≥ x + 1 = “Tồn tại số thực x không nhỏ hơn số ấy cộng với 1”. Mệnh đề này sai.
d) ∃x ∈ R: 3x = x2 + 1 = ∀x ∈ R: 3x ≠ x2 + 1 = “Tổng của 1 với bình phương của số thực x luôn luôn không bằng 3 lần số x”
Đây là mệnh đề sai vì với 
ta có : 
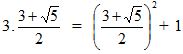
II- Phần Bài tập Tập hợp – Trang 13 SGK đại số 10
Bài số 1
a) Cho A = {x ∈ N| x < 20 và x chia hết cho 3}
Hãy liệt kê các phân tử của tập hợp A.
b) Cho tập hợp B = {2, 6, 12, 20, 30}.
Hãy xác định B bằng cách chỉ ra một tính chất đặc trưng cho các phần tử của nó.
c) Hãy liệt kê các phần tử của tập hợp các học sinh lớp em cao dưới 1m60.
Hướng dẫn giải:
a) A = {0, 3, 6, 9, 12, 15, 18}.
b) B = {x ∈ N / x = n(n + 1), n ∈ N, 1 ≤ n ≤ 5}.
c) Học sinh tự thực hiện.
Bài số 2
Trong hai tập hợp A và B dưới đây, tập hợp nào là con của tập hợp còn lại ? Hai tập hợp A và B có bằng nhau không?
a) A là tập hợp các hình vuông
B là tập hợp các hình thoi.
b) A = {n ∈ N / n là một ước chung của 24 và 30}
B = {n ∈ N/ n là một ước của 6}.
Hướng dẫn giải:
a) Mỗi hình vuông là một hình thoi (có một góc vuông). Vậy A ⊂ B, A ≠ B.
b) Mỗi số là ước của 6 là một ước chung của 24 và 30.
n ∈ B => n ∈ A. Vậy B ⊂ A. Mặt khác mỗi ước chung của 24 và 30 là một ước của 6. Vậy A ⊂ B. Suy ra A = B.
Bài số 3
Tìm tất cả các tập con của tập hợp sau:
a) A = {a, b};
b) B = {0, 1, 2}.
Hướng dẫn giải:
a) {a}, {b}, Ø, A.
b) {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, Ø, B.
Ghi chú: Tập hợp Ø là tập hợp con của tập hợp bất kì. Mỗi một tập hợp là tập hợp con của chính nó.
III- Các phép toán trong tập hợp – Bài tập 1,2,3,4 trang 15 đại số 10
Bài số 1
Kí hiệu A là tập hợp các chữ cái trong câu “CÓ CHÍ THÌ NÊN”, B là tập hợp các chữ cái trong câu “CÓ CÔNG MÀI SẮT CÓ NGÀY NÊN KIM’.
Hãy xác định A ∩ B, A ∪ B, A\B, B/A
Hướng dẫn giải:
A = {C, E, Ê, H, I, N, O, T}
B = {A, Ă, C, Ê, K, I, G, O, Ô, M, N, S, T, Y}
A ∩ B = {C, Ê, I, N, O, T}
A ∪ B = {A, Ă, C, E, Ê, G, H, I, K, M, N, O, Ô, S, T, Y}.
A\B = {H}.
B\A = {A, Ă, G, Ô, M, S, Y, K}
Bài số 2
Vẽ lại và gạch chéo các tập hợp A ∩ B, A ∪ B, A\B (h.9) trong các trường hợp sau:
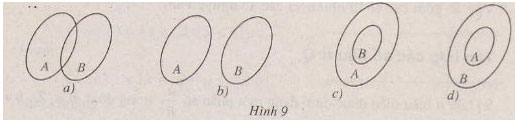Hướng dẫn giải:
a) Trường hợp thứ nhất, xem trong tóm tắt lí thuyết.
b)
c)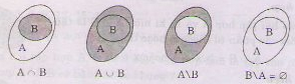 
d) Bạn nghiên cứu thêm, tự giải.
Bài số 3
Trong 45 học sinh của lớp 10A có 15 bạn được xếp loại học lực giỏi, 20 bạn được xếp loại hạnh kiểm tốt, trong đó có 10 bạn vừa học lực giỏi, vừa có hạnh kiểm tốt. Hỏi
a) Lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải có học lực giỏi hoặc hạnh kiểm tốt ?
b) Lớp 10A có bao nhiêu bạn chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt?
Hướng dẫn giải:
a) Gọi A là tập hợp học sinh giỏi, B là tập hợp học sinh được hạnh kiểm tốt của lớp 10A, thì A ∩ B là tập hợp các học sinh vừa giỏi, vừa có hạnh kiểm tốt.
Tập hợp học sinh được khen thưởng là A ∪ B. Số phân tử của A ∪ B bằng só phân tử của A cộng với số phân tử của B bớt đi số phân tử của A ∩ B (vì được tính hai lần).
– Vậy số học sinh lớp 10A được khen thưởng là:
15 + 20 – 10 = 25 người.
b) Số bạn lớp 10A chưa học giỏi và chưa có hạnh kiểm tốt là số học sinh lớp 10A chưa được khen thưởng bằng:
45 – 25 = 20 người.
Bài số 4
Cho tập hợp A, hãy xác định:
A ∩ A, A ∪ A, A ∩ Ø, A ∪ Ø, CAA, CAØ.
Hướng dẫn giải:
A ∩ A = A;
A ∪ A = A;
A ∩ Ø = Ø;
A ∪ Ø = A;
CAA = Ø;
CAØ = A;
IV- Chương 1 số gần đúng – sai số: bài tập 1,2,3,4,5 trang 23 SGK đại số 10
Bài số 1
Biết 3√5 = 1,709975947 …
Viết gần đúng 3√5 theo nguyên tắc làm tròn với hai, ba, bốn chữ số thập phân và ước lượng sai số tuyệt đối.
Hướng dẫn giải:
3√5 ≈ 1,71 với sai số mắc phải 0,01;
3√5 ≈ 1,710 với sai số mắc phải 0,001;
3√5 ≈ 1,7100 với sai số mắc phải 0,0001
Bài số 2
Chiều dài một cái cầu là l = 1745,25 m ± 0,01 m.
Hãy viết số quy tròn của số gần đúng 1745,25.
Hướng dẫn giải:
Độ chính xác của số đo là 1/100 m. Chữ số 5 ở hàng phần trăm nên không đáng tin ta phải bỏ và theo quy tắc làm tròn.
Cộng thêm 1 đơn vị vào hàng kế tiếp (2 + 1 = 3).
Tóm lại các chữ số đáng tin là 1; 7; 4; 5; 2 và chiều dài cầu viết dưới dạng chuẩn là d = 1745,30.
Bài số 3
a) Cho giá trị gần đúng của π là a = 3,141592653589 với độ chính xác là 10-10. Hãy viết số quy tròn của a;
b) Cho b = 3,14 và c = 3,1416 là những giá trị gần đúng của π. Hãy ước lượng sai số tuyệt đối của b và c.
Hướng dẫn giải:
a) Dạng chuẩn của số π với 10 chữ số chắc là 3,141592654 với sai số tuyệt đối ∆π ≤ 10-9.
b) Viết π ≈ 3,14 ta mắc phải sai số tuyệt đối không quá 0,002. Trong cách viết này có 3 chữ số đáng tin.
Viết π ≈ 3,1416 ta mắc phải sai số tuyệt đối không quá 10-4. Viết như vậy thì số π này có 5 chữ số đáng tin.
Bài số 4
Thực hiện các phép tính sau trên máy tính bỏ túi (trong kết quả lấy 4 chữ số ở phần thập phân).
a) 37.√14;
b) 3√15.124.
Hướng dẫn giải:
a). Nếu dùng máy tính CASIO fx-500 MS ta làm như sau:
Bạn ấn 
, ấn liên tiếp phím 
khi màng hình hiện ra 
Ấn liên tiếp 
để lấy 4 chữ số phần thập phân. Kết quả hiện ra trên màn hình là 8183.0047.
b) 
Kết quả là 51139.3736.
Bài số 5
Thực hiện các phép tính sau trên máy tính bỏ túi
a) 3√217: 135 với kết quả có 6 chữ số thập phân;
b) (3√42+ 5√37) : 145 với kết quả có 7 chữ số thập phân;
c) [(1,23)5 + 3√-42]9 với kết quả có 5 chữ số thập phân.
Hướng dẫn giải:
a) Nếu dùng máy tính CASIO fx-500 MS ta làm như sau:
Ấn 
Ấn liên tục phím khi màng hình hiện ra
Ấn liên tiếp 
để lấy chữ số thập phân.
Kết quả hiện ra trên màn hình là 0.000016.
b) 
, Kết quả 1029138.10-5
c) 
, Kết quả: -2,3997.10-2.
V – Ôn tập chương 1 – Trang 24, 25 đại số 10
Bài số 1
Xác định tính đúng sai của mệnh đề phủ định Ā theo tính đúng sai của mệnh đề A.
Hướng dẫn giải
| A | Ā |
| Đ | S |
| S | Đ |
- Ā sai nếu A đúng
- Ā đúng nếu A sai
Bài số 2
Thế nào là mệnh đề đảo của mệnh A ⇒ B? Nếu A ⇒ B là mệnh đề đúng, thì mệnh đề đảo của nó có đúng không? Cho ví dụ minh họa.
Hướng dẫn giải bài:
Mệnh đề đảo của A ⇒ B là B ⇒ A
A ⇒ B đúng chưa chắc B ⇒ A đúng.
Ví dụ: A: hai góc đối đỉnh; B: hai góc ấy bằng nhau Ta có: A ⇒ B đúng. Xét B ⇒ A: nếu hai góc bằng nhau thì hai góc ấy đối đỉnh. Mệnh đề này sai.
Bài số 3
Thế nào là hai mệnh đề tương đương?
Hướng dẫn giải:
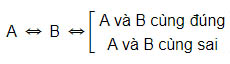
Bài số 4
Nêu định nghĩa tập hợp con và định nghĩa hai hợp bằng nhau.
Hướng dẫn giải:
A⊂B ⇔ ∀x (x ∈ A ⇒ x ∈ B)
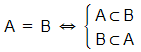
Bài số 5
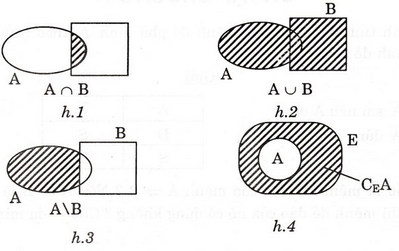
Nêu các định nghĩa hợp, giao, Hiệu và phần bù của hai tập hợp. Minh họa các khái niệm đó bằng hình vẽ.
Hướng dẫn giải:
A ∩ B ⇔ ∀x (x ∈ A và x ∈ B) (h.1)
A ∪ B ⇔ ∀x (x ∈ A hoặc x ∈ B) (h.2)
A \ B ⇔ ∀x (x ∈ A hoặc x ∉ B) (h.3)
Cho A ⊂ E.CEA = {x/x ∈ E và x ∉ A} (h.4)
Bài số 6
Nêu định nghĩa đoạn [a; b], khoảng (a; b), nửa khoảng [a; b), (a; b], (-∞; b], [a; +∞). Viết tập hợp R các số thực dưới dạng một khoảng.
Hướng dẫn giải:
x ∈ [a; b] ↔ a ≦ x ≦ b.
x ∈ (a; b) ↔ a < x < b.
x ∈ [a; b) ↔ a ≦ x < b.
x ∈ (a; b] ↔ a < x ≦ b.
x ∈ [a; b] ↔ a ≦ x ≦ b.
x ∈ (-∞; b] ↔ x ≦ b.
x ∈ [a; +∞] ↔ a ≦ x.
x ∈ R ↔ x ∈ (-∞; +∞).
Bài số 7
Thế nào là sai số tuyệt đối của một số gần đúng? Thế nào là độ chính xác của một số gần đúng?
Hướng dẫn giải:
Gọi a là số gần đúng; ā là số đúng của số đo của một đại lượng.
Sai số tuyệt đối của a là: Δa = |ā – a|
Nếu Δa = |ā – a| ≤ h thì h được gọi là độ chính xác của số gần đúng.
(Ta còn viết: a-h ≤ ā ≤ a+h)
Bài số 8
Cho tứ giác ABCD. Xét tính đúng sai của mệnh đề P ⇒ Q với
a) P: “ABCD là một hình vuông”
Q: “ABCD là một hình bình hành”
b) P: “ABCD là một hình thoi”
Q: “ABCD là một hình chữ nhật”
Hướng dẫn giải:
a) Đúng;
b) Sai;
Bài số 9
Xét mối quan hệ bao hàm giữa các tập hợp sau
A là tập hợp các hình tứ giác;
B là tập hợp các hình bình hành;
C là tập hợp các hình thang;
D là tập hợp các hình chữ nhật;
E là tập hợp các hình vuông;
G là tập hợp các hình thoi.
Hướng dẫn giải:
Hình vuông là hình chữ nhật …………….. nên E ⊂ D
Hình chữ nhật là hình bình hành…………….. nên D ⊂ B
Hình bình hành là hình thang…………….. nên B ⊂ C
Hình thang là hình tứ giác …………….. nên C ⊂ A
Vậy, A ⊃ C ⊃ B ⊃ D ⊃ E
Mặt khác:
– Hình vuông là hình thoi …………….. nên E ⊂ G
Hình thoi là hình bình hành………………. nên G ⊂ B
Vậy, A ⊃ C ⊃ B ⊃ G ⊃ E.
Bài số 10
Liệt kê các phần tử của mỗi tập hợp sau
a) A = {3k – 2 | k = 0, 1, 2, 3, 4, 5};
b) B = {x ∈ N |x ≤ 12}
c) C = {(1 – n)n | n ∈ N}
Hướng dẫn giải:
a) Khi:
k = 0 thì 3k – 2 = -2
k = 1 thì 3k – 2 = 1
k = 2 thì 3k – 2 = 4
k = 3 thì 3k – 2 = 7
k = 4 thì 3k – 2 = 10
k = 5 thì 3k – 2 = 13
Nên A = {-2; 1; 4; 7; 10; 13}
b) Vì x ∈ N và x ≦ 12 nên x = 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12
Vậy B = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
c) Vì n ∈ N nên n = 0; 1; 2;…
Do đó, (-1)n = 1 khi n = 0 hay n chẵn
(-1)n = -1 khi n lẻ
Vậy, C = {-1; 1}
Bài số 11
Giả sử A, B là hai tập hợp số và X là một số đã cho. Tìm các cặp mệnh đề tương đương trong các mệnh đề sau
P: “x ∈ A ∪ B”; S: “x ∈ A và x ∈ B”;
Q: “x ∈ A \ B”; T: “x ∈ A hoặc x ∈ B”;
R: “x ∈ A ∩ B”; X:”x ∈ A hoặc x ∉ B”
Hướng dẫn giải:
P ⇔ T; R ⇔ S; Q ⇔ X
Bài số 12
Xác định các tập hợp sau:
a) (-3; 7) ∩ (0; 10);
b) (—∞; 5) ∩ (2; +∞);
c) R \(—∞; 3)
Hướng dẫn giải:
Bài số 13
Dùng máy tính bỏ túi hoặc bảng kẻ số để tìm giá trị của 3√12 Làm tròn kết quả nhận được đến chữ số thập phân thứ ba và ước lượng sai số tuyệt đối.
Hướng dẫn giải:
- Kết quả đã làm tròn: 3√12 ≈ 2,289
- Ước lượng sai số tuyệt đối: |2,289 – 2,289| < 0,001
Bài số 14
Chiều cao của một ngọn đồi đo được là h = 347,13 ± 0,2m. Hãy viết số quy tròn của số gần đúng 347,13
Hướng dẫn giải:
Số quy tròn của h = 347,13 ± 0,02 (m) là h = 347.
Bài số 15
Những quan hệ nào trong các quan hệ sau là đúng?
a) A ⊂ A ∪ B; b)A ⊂ A ∩ B;
c)A ∩ B ⊂ A ∪ B; d)A ∪ B ⊂ B;
e) A ∩ B ⊂ A.
Hướng dẫn giải:
a. Đúng
b. Sai (vì X ∈ A không thể suy ra X ∈ A ∩ B)